OOPSLA 2006 Educator's Symposium: Nifty Assignment
Temperature Calculator
Programming for Change
Dung “Zung” Nguyen, Mathias Ricken
Rice University , Houston, TX USA
Website with Applets and Updated Materials
A version of this document with working applets and updated materials is available at:
http://ricken.us/research/tempcalc/website
Archive
Download all solutions as ZIP file
Solutions
Exercise 1a: Identify the variant and the invariant of converting a temperature from Celsius to Fahrenheit.
The variant is the numeric value of the temperature. The invariant is the conversion formula from Celsius to Fahrenheit.
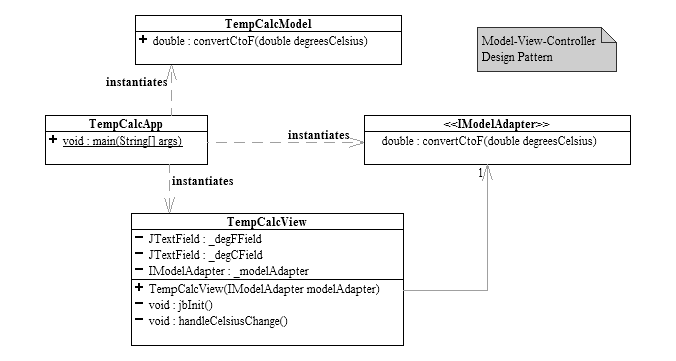
Exercise 1b: Draw a UML diagram of the model. It should consist of a single static method.
This is the UML diagram of the entire program. The model consists of just the TempCalcModel class.
Exercise 1c: Write a program that allows the user to convert any temperature in Celsius to its corresponding value in Fahrenheit. You can start by modifying the code for the constant solution, but remember to provide the two user interfaces! Watch out for integer arithmetic being carried out instead of floating point arithmetic.
Exercise 2a: Draw a UML diagram of a changed model that consists of two static methods and allows conversion in both directions.
This is the UML diagram of just the model. The rest of the program is similar to the one depicted in Exercise 1b.
Exercise 2b: Write a program that implements this design. Again, provide two user interfaces.
Exercise 3a: If you follow the pattern from the first two solutions of using one static method per possible conversion, how many methods will you need for this model?
There are three temperature scales, each needing conversion functions to the two other scales: 3*2 = 6.
Exercise 3b: Draw the UML diagram of the changed model, with one static method for each possible conversion.
This is the UML diagram of just the model. The rest of the program is similar to the one depicted in Exercise 1b.
Exercise 3c: Write a program that implements this design. Again, provide two user interfaces.
Exercise 4a: Compare the model from Exercise 2 to the model from Exercise 3. What is the ration between the number of methods in the models of Exercise 2 and Exercise 3?
The model for Exercise 2 required two methods; the one for Exercise 3 six. The ratio is 1:3.
Exercise 4b: Assume we added full support for the Reaumur scale to our program. Using our current approach of one method per possible conversion, how many methods will you need?
There are four temperature scales, each needing conversion functions to the three other scales: 4*3 = 12.
Exercise 4c: Using your answers to Exercises 3a, 4a and 4b, derive a formula - f - that allows you to calculate the number of methods, given the number of temperature scales - n: f(n) =
Each of the n temperature scales needs conversion functions to the n-1 other scales. Therefore, f(n) = n*(n-1).
Exercise 4d: What is the complexity (i.e. the number of methods) of this approach, expressed in "big O" notation?
f(n) = n*(n-1) = n2-n. The dominating term is n2, therefore the number of methods is in O(n2). The size of the program grows quadratically.
Exercise 5a: Using this new approach, what is the minimum number of methods we need to convert between three scales? Four scales? n scales?
Except for the first scale, which serves as a connection between the scales, every scale needs two conversion functions: to the first scale and back. The first scale doesn't need any conversions.
Three scales: 4 methods
Four scales: 6 methods
n scales: 2*(n-1) methods
Exercise 5b: What is the complexity (i.e. the number of methods) of this new approach, expressed in "big O" notation?
The dominating term of 2*(n-1) = 2n - 2 is 2n. Therefore, the number of methods is in O(n) and we have achieved linear growth.
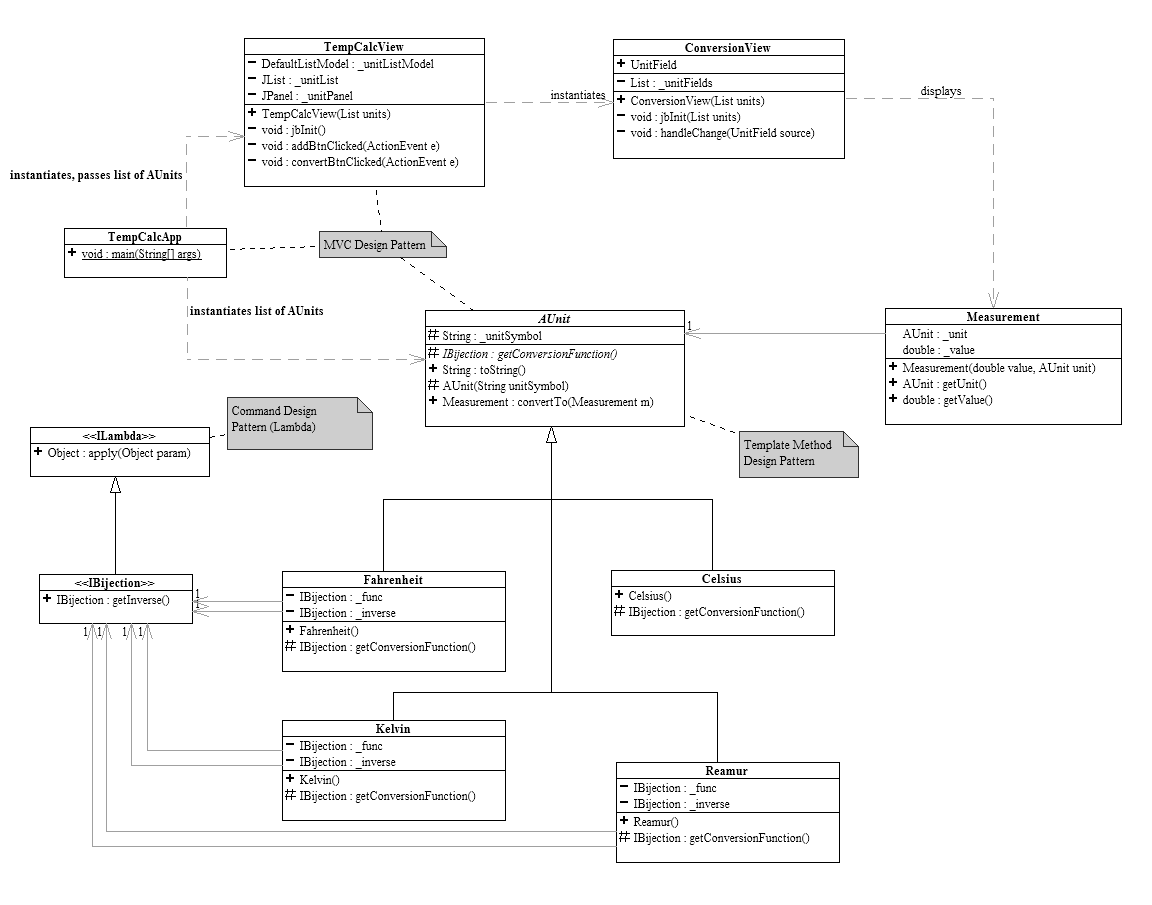
Exercise 5c: Draw a UML diagram of the model using the new approach. The model should have the minimum number of methods to still perform arbitrary conversions between Celsius, Fahrenheit, and Kelvin.
This is the UML diagram of just the model. The rest of the program is similar to the one depicted in Exercise 1b.
Exercise 5d: Write a program that implements this design. Again, provide two user interfaces; they should look the same as in the program for Exercise 3c.
Exercise 6a: What differs and what always remains the same when performing conversions this way? Identify the variants and the invariants. Remember that we can pass functions as data in an object-oriented language like Java.
The variant is the choice of the two conversion functions: the function to convert to the base scale, and the function to convert back from the base scale. The invariant is the process of applying the input value to the first function, and then applying its result to the second function to obtain the final result.
Exercise 6b: What three pieces of data are necessary to define a temperature scale in our model? Hint: These are the invariants you identified earlier.